Math Cheatsheet
此页面含有大量巨型数学公式,在移动设备上打开时可能会出现问题。
常用麦克劳林展开与常用等价无穷小
当 \(x\to 0\) 时,
\(\mathrm{e}^x=1+x+\dfrac{x^2}{2!}+\dfrac{x^3}{3!}+\cdots\);
\(x\sim \mathrm{e}^x-1\);
\(a\) 是常数,则 \(a^x=1+x\ln a+\dfrac{x^2\ln^2a}{2!}+\cdots\)。
\(\ln(1+x)=x-\dfrac{x^2}{2}+\dfrac{x^3}{3}-\cdots\);
\(x\sim\ln(1+x)\);
\(a\) 是常数,则 \(\log_a(1+x)=\dfrac{x}{\ln a}-\dfrac{x^2}{2\ln^2a}+\cdots\)。
\((1+x)^n=1+nx+\dfrac{n(n-1)}{2!}x^2+\dfrac{n(n-1)(n-2)}{3!}x^3+\cdots\);
\((1+x)^n\sim1+nx\);
将 \(x\) 替换为 \(-x\),得到 \((1-x)^n=1-nx+\dfrac{n(n-1)}{2!}x^2-\cdots\)。
\(\dfrac{1}{1-x}=1+x+x^2+x^3+\cdots\);
即是等比数列求和公式;
将 \(-x\) 替换为 \(x\),得到 \(\dfrac{1}{1+x}=1-x+x^2-x^3+\cdots\)。
\(\sin x=x-\dfrac{x^3}{3!}+\dfrac{x^5}{5!}-\dfrac{x^7}{7!}+\cdots\);
\(x\sim\sin x\);
\(x-\sin x\sim\dfrac{1}6x^3\)。
\(\cos x=1-\dfrac{x^2}{2!}+\dfrac{x^4}{4!}-\dfrac{x^6}{6!}+\cdots\);
\(\cos x\sim1-\dfrac{x^2}{2}\)。
\(\tan x=x+\dfrac{x^3}{3}+\dfrac{2}{15}x^5+\cdots\);
通项非常复杂,记住 \(\dfrac{1}3\) 和 \(\dfrac{2}{15}\) 就行;
\(x\sim\tan x\);
\(x-\tan x\sim-\dfrac{1}3x^3\);
\(\sin x-\tan x\sim-\dfrac{1}2x^3\)。
\(\arcsin x=x+\dfrac{x^3}{6}+\dfrac{3x^5}{40}+\cdots\);
同样地,通项非常复杂,记住 \(\dfrac{1}{6}\) 和 \(\dfrac{3}{40}\) 就行;
\(x\sim\arcsin x\);
\(x-\arcsin x\sim-\dfrac{1}{6}x^3\);
由诱导公式得 \(\arccos x=\dfrac{\pi}{2}-\arcsin x\)。
\(\arctan x=x-\dfrac{x^3}{3}+\dfrac{x^5}{5}-\dfrac{x^7}{7!}+\cdots\)。
\(x\sim\arctan x\);
\(x-\arctan x\sim-\dfrac{x^3}{3}\)。
常用结构求导
常见函数的导函数公式这里不再整理。下面是一些常见结构的求导。
\(\left(\dfrac{1}{x}\right)'=-\dfrac{1}{x^2}\);
\((\sqrt{x})'=\dfrac{1}{2\sqrt{x}}\);
\((xf(x))'=f(x)+xf'(x)\);
特别地,\((x\mathrm{e}^x)'=(x+1)\mathrm{e}^x\),而 \((x\ln x)'=\ln x+1\)。
如果将「\(+\)」换成「\(-\)」,考虑 \(\left(\dfrac{f(x)}{x}\right)'=\dfrac{xf'(x)-f(x)}{x^2}\)。
\(\left(\ln(x+\sqrt{a+x^2})\right)'=\dfrac{1}{\sqrt{a+x^2}}\),其中 \(a\) 是常数。
有等价无穷小:当 \(x\to 0\) 时,\(x\sim\ln(x+\sqrt{1+x^2})\)。
\((\dfrac{1}2f^2(x))'=f(x)f'(x)\);
可以构造出原函数与函数自己的乘积项。
\(\left(x+\dfrac{1}x\right)'=1-\dfrac{1}{x^2}\)
积分常用。
常用不定积分(一)
以下积分公式是由常见函数的导函数公式直接得来的。
\(\int0\mathrm{d}x=C\);
\(\int 1\mathrm{d}x=x+C\);
\(\int x^\mu\mathrm{d} x=\dfrac{1}{\mu+1}x^{\mu+1}+C\),其中 \(\mu\ne-1\);
\(\int\dfrac{1}{x}\mathrm{d}x=\ln|x|+C\),其中 \(x\neq0\);
\(\int a^x\mathrm{d}x=\dfrac{1}{\ln a}a^x+C\),其中 \(a>0, a\ne 1\);
\(\int\mathrm{e}^x\mathrm{d}x=\mathrm{e}^x+C\);
\(\int\sin x\mathrm{d}x=-\cos x+C\);
\(\int\cos x\mathrm{d} x=\sin x+C\);
\(\int\sec^2x\mathrm{d}x=\tan x+C\);
\(\int\csc^2x\mathrm{d}x=-\cot x+C\);
\(\int\sec x\tan x\mathrm{d}x=\int\dfrac{\sin x}{\cos^2x}\mathrm{d}x=\sec x+C\);
\(\int\csc x\cot x\mathrm{d}x=\int\dfrac{\cos x}{\sin^2x}\mathrm{d}x=-\csc x+C\);
\(\int\dfrac{\mathrm{d}x}{\sqrt{1-x^2}}=\arcsin x+C\);
\(\int\dfrac{\mathrm{d}x}{1+x^2}=\arctan x+C\)。
常用不定积分(二)
以下积分公式是由三角函数变换得到的。
\(\int\tan x\mathrm{d}x=-\ln|\cos x|+C\);
推导:\(\int\tan x\mathrm{d}x=\int\dfrac{\sin x}{\cos x}\mathrm{d}x=\int\dfrac{-\mathrm{d}\cos x}{\cos x}=-\ln|\cos x|+C\)。
少见的 \(\tan x\) 和 \(\cos x\) 配对。
\(\int\cot x\mathrm{d}x=\ln|\sin x|+C\);
推导:\(\int\cot x\mathrm{d}x=\int\dfrac{\cos x}{\sin x}\mathrm{d}x=\int\dfrac{\mathrm{d}\sin x}{\sin x}=\ln|\sin x|+C\)。
\(\int\sec x\mathrm{d}x=\ln|\sec x+\tan x|+C\);
推导如下:
\[\begin{aligned}\int\sec x\mathrm{d}x&=\int\dfrac{1}{\cos x}\mathrm{d}x=\int\dfrac{\cos x}{\cos^2x}\mathrm{d}x=\int\dfrac{\mathrm{d}\sin x}{1-\sin^2x}\\&=\dfrac{1}2\int\left(\dfrac{1}{1-\sin x}+\dfrac{1}{1+\sin x}\right)\mathrm{d}\sin x\\&=\dfrac{1}2\ln\left|\dfrac{1+\sin x}{1-\sin x}\right|+C=\dfrac{1}2\ln\left|\dfrac{(1+\sin x)^2}{\cos^2x}\right|+C\\&=\ln\left|\dfrac{1}{\cos x}+\dfrac{\sin x}{\cos x}\right|+C=\ln|\sec x+\tan x|+C。\end{aligned}\]
\(\int\csc x\mathrm{d}x=\ln|\csc x-\cot x|+C\);
推导如下:
\[\begin{aligned}\int\csc x\mathrm{d}x&=\int\dfrac{1}{\sin x}\mathrm{d}x=\int\dfrac{\sin x}{\sin^2x}\mathrm{d}x=-\int\dfrac{\mathrm{d}\cos x}{1-\cos^2x}\\&=-\dfrac{1}2\int\left(\dfrac{1}{1-\cos x}+\dfrac{1}{1+\cos x}\right)\mathrm{d}\cos x\\&=-\dfrac{1}2\ln\left|\dfrac{1+\cos x}{1-\cos x}\right|+C=\dfrac{1}2\ln\left|\dfrac{(1-\cos x)^2}{\sin^2x}\right|+C\\&=\ln\left|\dfrac{1}{\sin x}-\dfrac{\cos x}{\sin x}\right|+C=\ln|\csc x-\cot x|+C。\end{aligned}\]
\(\int\dfrac{\mathrm{d}x}{x^2+a^2}=\dfrac{1}a\arctan\dfrac{x}{a}+C\);
推导:\(\int\dfrac{\mathrm{d}x}{x^2+a^2}=\dfrac{1}{a}\int\dfrac{\mathrm{d}\dfrac{x}{a}}{\left(\dfrac{x}{a}\right)^2+1}=\dfrac{1}a\arctan\dfrac{x}{a}+C\)。
\(\int\dfrac{\mathrm{d}x}{x^2-a^2}=\dfrac{1}{2a}\ln\left|\dfrac{x-a}{x+a}\right|+C\);
推导:\(\int\dfrac{\mathrm{d}x}{x^2-a^2}=\dfrac{1}{2a}\int\left(\dfrac{1}{x+a}-\dfrac{1}{x-a}\right)\mathrm{d}x=\dfrac{1}{2a}\ln\left|\dfrac{x-a}{x+a}\right|+C\)。
\(\int \dfrac{1}{\sqrt{a^2-x^2}} \mathrm{d}x=\arcsin \dfrac{x}a+C\);
推导:\(\int\dfrac{1}{\sqrt{a^2-x^2}}\mathrm{d}x=\int\dfrac{\mathrm{d}\dfrac{x}{a}}{\sqrt{1-\left(\dfrac{x}{a}\right)^2}}=\arcsin\dfrac{x}{a}+C\)。也可考虑另外一种做法。构造下面这个直角三角形:
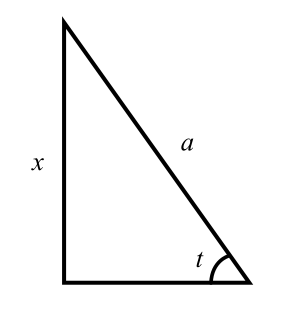
其中 \(t\in\left(-\dfrac{\pi}2, \dfrac{\pi}2\right)\),则 \(x=a\sin t, \sqrt{a^2-x^2}=a\cos t\)。于是,\(\int\dfrac{1}{\sqrt{a^2-x^2}}\mathrm{d}x=\int\dfrac{1}{a\cos t}\cdot a\cos t\mathrm{d}t=t+C=\arcsin{\dfrac{x}{a}}+C\)。
\(\int\dfrac{1}{\sqrt{x^2\pm a^2}}\mathrm{d}x=\ln|x+\sqrt{x^2\pm a^2}|+C\);
先考虑取 \(+\) 的情况。构造下面的直角三角形:
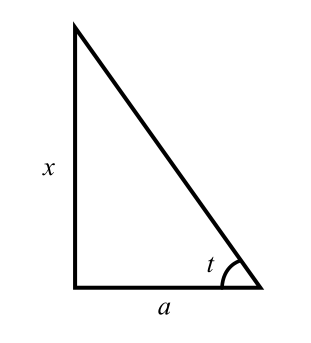
令 \(x=a\tan t\),其中 \(t\in\left(-\dfrac{\pi}2, \dfrac{\pi}2\right)\)。有 \(\sqrt{x^2+a^2}=a\sec t\)。则 \(\int\dfrac{1}{\sqrt{x^2+a^2}}\mathrm{d}x=\int\dfrac{1}{a\sec t}\cdot a\sec^2t\mathrm{d}t=\int\sec t\mathrm{d}t=\ln|\sec t+\tan t|+C_1\)。又 \(\sec t=\dfrac{\sqrt{x^2+a^2}}{a}\),\(\tan t=\dfrac{x}a\),所以上式变为 \(\ln\left|\dfrac{x+\sqrt{x^2+a^2}}{a}\right|+C_1\)。将分母的 \(a\) 划入常数项,得到 \(\ln|x+\sqrt{x^2+a^2}|+C\)。
取 \(-\) 的情况类似。
\(\int\sqrt{a^2-x^2}\mathrm{d}x=\dfrac{x}2\sqrt{a^2-x^2}+\dfrac{a^2}2\arcsin\dfrac{x}a+C\);
构造下面的直角三角形:

有 \(t\in\left(-\dfrac{\pi}2, \dfrac{\pi}2\right)\),容易得到 \(x=a\sin t, \sqrt{a^2-x^2}=a\cos t\)。有
\[\begin{aligned} \int\sqrt{a^2-x^2}\mathrm{d}x&=a^2\int\cos^2t\mathrm{d}t=\dfrac{a^2}{2}\int\dfrac{\cos 2t+1}{2}\mathrm{d}t\\ &=\dfrac{a^2}{4}\left(\sin2t+2t\right)=\dfrac{a^2t}{2}+\dfrac{a^2\sin2t}{4},\end{aligned}\]
而 \(t=\arcsin\dfrac{x}{a}\),\(\sin2t=2\sin t\cos t=\dfrac{2x\sqrt{a^2-x^2}}{a^2}\),代入得到答案。
\(\int\sqrt{x^2\pm a^2}\mathrm{d}x=\dfrac{x}{2}\sqrt{x^2\pm a^2}\pm\dfrac{a^2}{2}\ln|x+\sqrt{x^2\pm a^2}|+C\);
这里只计算取 \(+\) 的情况。构造下面的直角三角形:

其中 \(t\in\left(-\dfrac{\pi}{2}, \dfrac{\pi}2\right)\),有 \(\sqrt{x^2+a^2}=a\sec t, x=a\tan t\)。故
\[\begin{aligned} \int\sqrt{x^2+a^2}\mathrm{d}x&=\int a\sec t\cdot a\sec^2t\mathrm{d}t=a^2\int\sec^3t\mathrm{d}t\\&= \dfrac{a^2}{2}(\tan t\sec t+\ln|\tan t+\sec t|)+C,\end{aligned}\]
其中 \(\tan t=\dfrac{x}{a}\),\(\sec t=\dfrac{\sqrt{x^2+a^2}}{x}\)。代入得到结果。
\(\int\sec^3 t\mathrm{d}t\) 用分部积分法求。记 \(I=\int\sec^3t\mathrm{d}t\),得到
\[\begin{aligned} I&=\int\sec^3t\mathrm{d}t=\int\sec t\mathrm{d}\tan t=\sec t\tan t-\int\tan t\mathrm{d}\sec t \\ &=\sec t\tan t-\int\tan^2t\sec t\mathrm{d}t=\sec t\tan t-\int\dfrac{\sin^2t}{\cos^3t}\mathrm{d}t\\&=\sec t\tan t-\int\dfrac{1-\cos^2t}{\cos^3t}\mathrm{d}t=\sec t\tan t-\int\sec^3t\mathrm{d}t+\int\sec t\mathrm{d}t \\ &=\sec t\tan t-I+\ln|\sec t+\tan t|+C_1, \end{aligned}\]
于是 \(I=\dfrac{1}{2}(\sec t\tan t+\ln|\sec t+\tan t|)+C\)。
当然这个式子本身也可以直接使用分部积分法计算:
\[\begin{aligned} \int\sqrt{x^2+a^2}\mathrm{d}x&=x\sqrt{x^2+a^2}-\int\dfrac{x^2\mathrm{d}x}{\sqrt{x^2+a^2}}=x\sqrt{x^2+a^2}-\int\dfrac{(x^2+a^2-a^2)\mathrm{d}x}{\sqrt{x^2+a^2}} \\&=x\sqrt{x^2+a^2}-\int\sqrt{x^2+a^2}\mathrm{d}x+a^2\int\dfrac{\mathrm{d}x}{\sqrt{x^2+a^2}}\\&=x\sqrt{x^2+a^2}+a^2(\ln|x+\sqrt{x^2+a^2}|+C_1),\end{aligned}\]
于是直接得到结果。
分部积分法常见结构
对于指数函数、三角函数、幂函数,它们作为 \(u\) 即「移出」的一方。
\(\mathrm{e}^{ax}\sin bx\) 和 \(\mathrm{e}^{ax}\cos bx\);
考虑指数函数求导为自身的特性。以前者为例,有 \(\int\mathrm{e}^{ax}\sin bx\mathrm{d}x=\dfrac{1}{a}\mathrm{e}^{ax}\sin bx-\dfrac{b}{a}\int\mathrm{e}^{ax}\cos bx\mathrm{d}x\)。再对 \(\dfrac{b}a\int \mathrm{e}^{ax}\cos bx\mathrm{d}x\) 用一次分部积分即可解出。
\(P_m(x)\,\mathrm{e}^{ax}\),其中 \(P_m(x)\) 表示 \(m\) 次多项式;
\(\int P_m(x)\,\mathrm{e}^{ax}=\dfrac{1}{a}\mathrm{e}^{ax}P_m(x)-\dfrac{1}{a}\int P_{m-1}(x)\,\mathrm{e}^{ax}\mathrm{d}x\),然后继续解后半部分。
\(P_m(x)\sin bx\) 和 \(P_m(x)\cos bx\);
利用 \(\sin x\) 和 \(\cos x\) 求导得对方的性质。\(\int P_m(x)\sin bx\mathrm{d}x=-P_m(x)\dfrac{1}b\cos bx+\dfrac{1}{b}\int P_{m-1}(x)\cos bx\mathrm{d}x\),然后继续解后半部分。
对于对数函数、反三角函数,它们作为 \(v\) 即「移入 \(\mathrm{d}\) 的一方」,因为它们的导数比自己简单。
\(P_m(x)(\ln x)^n\);
\(\int P_m(x)(\ln x)^n\mathrm{d}x=P_{m+1}(x)(\ln x)^n-n\int P_m'(x)(\ln n)^{n-1}\mathrm{d}x\),然后继续解后半部分。
\(P_m(x)\arctan x\);
\(\int P_m(x)\arctan x\mathrm{d}x=P_{m+1}(x)\arctan x-\int \dfrac{P_{m+1}(x)}{1+x^2}\mathrm{d}x\),然后解后半部分。
多项式分式的积分
假定分母都不能再因式分解。
\(\int\dfrac{\mathrm{d}x}{x^2+px+q}\),分母配方,分子化为 \(\mathrm{d}(x+c)\),用 \(\arctan x\) 处理。
\(\int\dfrac{x+c}{x^2+px+q}\mathrm{d}x\),分子化为 \(\mathrm{d}(x^2+px+q)\)。
万能代换
对于三角函数有理式(三角函数的四则运算),可以用半角公式代换。令 \(u=\tan\left(\dfrac{x}{2}\right)\),则
\[\left\{\begin{aligned}&\sin x=2\sin\dfrac{x}2\cos\dfrac{x}2=\dfrac{2\tan\left(\dfrac{x}2\right)}{\sec^2\left(\dfrac{x}2\right)}=\dfrac{2u}{1+u^2},\\ &\cos x=\cos^2\dfrac{x}2-\sin^2\dfrac{x}2=\dfrac{1-\tan^2\left(\dfrac{x}2\right)}{\sec^2\left(\dfrac{x}2\right)}=\dfrac{1-u^2}{1+u^2},\\&\mathrm{d}x=\dfrac{2}{1+u^2}\mathrm{d}u。\end{aligned}\right.\]
记住分母是 \((1+u^2)\)。
定积分常用公式
\(\int\limits_0^{\pi/2}\sin^nx=\int\limits_0^{\pi/2}\cos^nx=\left\{\begin{aligned}&\dfrac{(n-1)(n-3)\cdots2}{n(n-2)(n-4)\cdots3}, n=2k+1,\\&\dfrac{(n-1)(n-3)\cdots1}{n(n-2)(n-4)\cdots2}\cdot\dfrac{\pi}{2},n=2k;\end{aligned}\right.\)
\(\int\limits_{-\infty}^{+\infty}\mathrm{e}^{-x^2}\mathrm{d}x=\sqrt{\pi}\)