密码学 6:杂凑、消息验证码与数字签名
Hash 函数
Hash 函数的定义
杂凑(hash,音译哈希)函数是一个公开函数 \(H\),将任意长度的消息 \(M\) 映射为短的固定长度的值 \(H(M)\)。
Hash 函数具有如下的性质:
单向性:已知 \(h=H(x)\) 计算 \(x\) 计算上不可行。
抗弱碰撞性(抗第二原象):已知 \(x\),求 \(y\) 使得 \(H(x)=H(y)\) 计算上不可行。
抗强碰撞性(抗碰撞):计算上无法找出 \(x\) 和 \(x'\) 使得 \(H(x)=H(x')\)。
「安全的」hash 函数
Merkle 提出安全 hash 函数的一般结构:
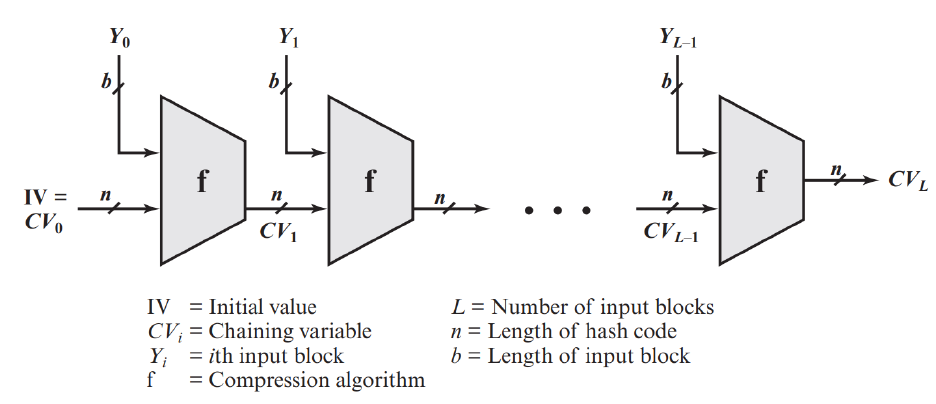
消息验证码
消息验证码(message authentication code, MAC)用来完成消息认证——验证消息来自正确的信源且没有被修改。它类似一种加密算法,需要通信双方事先共享密钥,但不一定可逆。
数字签名
数字签名的特性
可信的:任何人都能验证签名的有效性。
不可伪造的:除了签名者外,其他人伪造签名是困难的。
不可复制的:一消息一签名,签名不能挪用。
不可改变的:消息一旦改变,签名就会变化。
不可抵赖的:签名者事后不能否认自己的签名。
RSA 签名
与 RSA 加密完全一致。
选择两个大素数 \(p\) 和 \(q\),计算 \(n=pq\),\(\phi(n)=(p-1)(q-1)\)。选择随机整数 \(e\in(1, \phi(n))\),使得 \(\gcd(e, \phi(n))=1\)。计算 \(e\) 模 \(\phi(n)\) 的乘法逆 \(d\)。\((e, n)\) 公开,\(d\) 保留。
签名过程:对消息 \(m<n\),签名 \(s\equiv m^d\ (\mathrm{mod}\ n)\)。
验签过程:验证 \(m\equiv s^e\ (\mathrm{mod}\ n)\) 的正确性。
缺陷:
可以伪造随机消息的签名。
乘法同态。
慢。
ElGamal 签名
选择大素数 \(p\),找到它的本原根 \(g\),选择 \(x<p\) 作为私钥,计算 \(y=g^x\ (\mathrm{mod} p)\) 作为公钥。
对消息 \(m\),随机选择 \(k<p-1\),计算:
\(r=g^k\ \mathrm{mod}\ p\)(类似于 ElGamal 加密中的一次性密钥)
\(s=k^{-1}(H(m)-xr)\ \mathrm{mod}\ (p-1)\)(类似于一种密文)
验签过程为验证 \(y^rr^s\equiv g^{H(m)}\ \mathrm{mod}\ p\) 的正确性。
Schnorr 签名
随机选择大素数 \(p\geqslant 2^{512}\),\(q|(p-1)\geqslant 2^{160}\),取 \(p\) 的本原根 \(g\),随机选择 \(x\in (1, q)\) 作为私钥,计算 \(y\equiv g^x\ (\mathrm{mod}\ p)\) 为公钥。
对消息 \(m\),随机选择 \(k\in (1, q)\),计算
\(r=g^k\ \mathrm{mod}\ p\)
\(s=xe+k\ \mathrm{mod}\ q\),其中 \(e=H(r, m)\)
验签过程为验证 \(r=g^sy^{-e}\ \mathrm{mod}\ p\) 的正确性。