密码学 2:数学基础
模运算
同余
给定正整数 \(n\) 和整数 \(a\),若有 \(a=qn+r\)。称 \(q\) 为 \(a\) 除以 \(n\) 的商,\(r\) 为余数,记 \(r=a\ \mathrm{mod}\ n\),有 \(0\leqslant r<n\),\(q=\lfloor a/n\rfloor\)。
对于整数 \(a\) 和 \(b\),若有 \((a\ \mathrm{mod}\ n)=(b\ \mathrm{mod}\ n)\),称 \(a\) 和 \(b\) 是模 \(n\) 同余的,记作 \(a\equiv b\ (\mathrm{mod}\ n)\)。\(n\) 称为模数。
如果 \(a\equiv 0\ (\mathrm{mod}\ n)\),有 \(n|a\)。
同余的性质
若 \(n|(a-b)\),有 \(a\equiv b\ (\mathrm{mod}\ n)\)。
若 \(a\equiv b\ (\mathrm{mod}\ n)\),则 \(b\equiv a\ (\mathrm{mod}\ n)\)。
若 \(a\equiv b\ (\mathrm{mod}\ n)\),\(b\equiv c\ (\mathrm{mod}\ n)\),则 \(a\equiv c\ (\mathrm{mod}\ n)\)。
模运算的性质
运算 \(a\ \mathrm{mod}\ n\) 将整数 \(a\) 映射到集合 \(\{0, 1, \cdots, n-2, n-1\}\),在此集合之上的运算称为模运算。模运算具有如下的性质:
\(((a\ \mathrm{mod}\ n) + (b\ \mathrm{mod}\ n))\ \mathrm{mod}\ n=(a+b)\ \mathrm{mod}\ n\)
\(((a\ \mathrm{mod}\ n) - (b\ \mathrm{mod}\ n))\ \mathrm{mod}\ n=(a-b)\ \mathrm{mod}\ n\)
\(((a\ \mathrm{mod}\ n) \times (b\ \mathrm{mod}\ n))\ \mathrm{mod}\ n=(a\times b)\ \mathrm{mod}\ n\)
利用这些性质可以快速地进行一些计算。例如求 \(11^7\ \mathrm{mod}\ 13\)。因为 \(11^2\ \mathrm{mod}\ 13=4\),故
\[11^4\ \mathrm{mod}\ 13=((11^2\ \mathrm{mod} 13)\times (11^2\ \mathrm{mod} 13))\ \mathrm{mod}\ 13=16\ \mathrm{mod}\ 13=3\]
所以 \(11^7\ \mathrm{mod}\ 13=(4\times 3\times 11)\ \mathrm{mod}\ 13=2\)。
剩余类与乘法逆元
定义 \(Z_n\) 为比 \(n\) 小的非负整数的集合 \(Z_n=\{0, 1, \cdots, n-2, n-1\}\)。这个集合称为剩余类集,或模 \(n\) 的剩余类。
对于 \(a\in Z_n\),当且仅当 \(a\) 与 \(n\) 互质时,\(a\) 存在乘法逆元 \(a^{-1}\in Z_n\),使得 \(aa^{-1}\ \mathrm{mod}\ n=1\)。例如:对于 \(Z_8\),\(a=5\),\(a\) 的乘法逆元是 \(5\)。若 \(a=6\),则不存在乘法逆元。
扩展欧几里得算法
欧几里得算法又称辗转相除法,设 \(a\) 和 \(b\) 是两个正整数,有 \(\gcd(a, b)=\gcd(b, a\ \mathrm{mod}\ b)\)。重复利用上述结论,可以求出两个数的最大公因数。
考虑乘法逆的计算。由 \(aa^{-1}\equiv 1\ (\mathrm{mod}\ n)\),有 \(n|aa^{-1}-1\),即存在整数 \(k\) 使得 \(nk=aa^{-1}-1\),所以 \(aa^{-1}-nk=1\)。因此,找 \(a\) 的逆元的本质,是找出 \(ax+by=\gcd(a, b)=1\) 中的 \(x\) 和 \(y\)。例如,对于 \(a=4321\),\(b=1234\),我们先执行辗转相除法:
\[\begin{aligned} 4321&= 3\times 1234+619 \\ 1234 &= 1\times 619+615 \\ 619 &= 1\times 615 + 4\\ 615 &= 153\times 4+3 \\ 4 &= 1\times 3 + 1 \end{aligned}\]
将第一个式子改写成
\[\begin{equation}619=4321-3\times 1234\end{equation}\]
注意右边现在的形式是 \(\alpha\times 4321+\beta\times 1234\)。现在,将第二个式子改写成
\[\begin{equation}615=1234-1\times 619\end{equation}\]
再把 (1) 式的 619 代入右边,就得到
\[\begin{equation} 615=1234-1\times(4321-3\times 1234)=-1\times4321+4\times1234 \end{equation}\]
不断重复这个过程,最终得到 \(1=j\times 4321+k\times1234\)。过程如下
\[\begin{aligned} 4&=619-615=2\times4321-7\times1234 \\ 3&=615-153\times4 \\ &=(-1\times4321+4\times1234)-153\times(2\times4321-7\times1234) \\ &= -307\times4321+1075\times1234 \\ 1 &=309\times4321-1082\times1234 \end{aligned}\]
这样,我们就成功地找到了 \(x\) 和 \(y\)。但是——这距离我们要的「乘法逆」还有一点差距。对于 1234 关于 4321 的乘法逆,我们要找的是一个正数;而上面式子中和 1234 相乘的是 -1082,这显然不是我们要的东西。
我们可以进行下面的变换:
\[(4321-1082)\times1234=1234\times4321-309\times4321+1=925\times4321+1\]
即 \(3239\times1234-925\times4321=1\),所以乘法逆为 3239。事实上,就是在之前的 -1082 加上模 4321 得到的数字。
费马小定理
若 \(p\) 是素数,\(a\) 是正整数且 \(p\not| a\),则 \(a^{p-1}\equiv 1\ (\mathrm{mod}\ p)\)。例如:\(a=7\),\(p=19\),则 \(7^{18}\equiv 1\ (\mathrm{mod}\ p)\)。
写成另一种形式的费马小定理:若 \(p\) 是素数,\(a\) 是任意正整数,则 \(a^p\equiv a\ (\mathrm{mod}\ p)\)。
欧拉定理
先引入欧拉函数 \(\phi(n)\):对一个正整数 \(n\),\(\phi(n)\) 为小于 \(n\) 且与 \(n\) 互素的正整数的个数。定义 \(\phi(1)=1\)。
例如:\(\phi(12)=4\),因为小于 12 并与 12 互素的正整数有 1、5、7、11 共 4 个。对于素数 \(p\),\(\phi(p)=p-1\)。如果一个正整数 \(n\) 可以表示成两个素数的乘积 \(pq\),则 \(\phi(n)=(p-1)(q-1)\)。
欧拉定理:若 \(a\) 与 \(n\) 互素,则 \(a^{\phi(n)}\equiv 1\ (\mathrm{mod}\ n)\)。类似费马小定理,也可以表述为 \(a^{\phi(n)+1}\equiv a\ (\mathrm{mod}\ n)\)(不要求互素)。
孙子定理 / 中国剩余定理
孙子定理最早见于《孙子算经》,作者 不是 《孙子兵法》的作者孙武:
今有物不知其数,三三数之有二,五五数之有三,七七数之有二,问物有多少?
即求未知数 \(x\),满足
\[\left\{\begin{aligned} & x \equiv 2\ (\mathrm{mod}\ 3) \\ & x \equiv 3\ (\mathrm{mod}\ 5) \\ & x \equiv 2\ (\mathrm{mod}\ 7) \\ \end{aligned}\right.\]
宋朝数学家秦九韶具体给出了此类同余方程组问题的解法,载于《数书九章》。对于模数为 3、5 和 7 的「物不知数」问题,将除以 3 的余数乘以 70,除以 5 的余数乘以 21,除以 7 的余数乘以 15,全部相加再除以 105,余数就是可行解。
对于此类问题,设 \(m_1, m_2, \cdots, m_k\) 是两两互素的正整数,\(M\) 是它们的乘积,则一次同余方程组
\[\left\{\begin{aligned} & x\equiv a_1\ (\mathrm{mod}\ m_1) \\ & x\equiv a_2\ (\mathrm{mod}\ m_2) \\ &\cdots \\ & x\equiv a_k\ (\mathrm{mod}\ m_k) \\ \end{aligned}\right.\]
有解。令 \(M_i=\frac{M}{m_i}\),则
\[x\equiv(M_1e_1a_1+M_2e_2a_2+\cdots+M_ke_ka_k)(\mathrm{mod}\ M)\]
其中 \(e_i\) 是 \(M_i\) 模 \(m_i\) 的乘法逆。因为 \(M_i\) 和 \(m_i\) 必然互素,因此乘法逆必然存在。
孙子定理提供了一个特性:在大模 \(M=\prod_{i=1}^km_i\) 下,可以将大数 \(A\) 用一组小数 \((a_1, a_2,\cdots, a_k)\) 表示。并且,对于这个大数的模运算,可以用这一组小数进行。例如,计算 \(17^2\ \mathrm{mod}\ 35\),使用 \(m_1=5, m_2=7\),有
\[\left\{\begin{aligned} & 17\equiv2\ (\mathrm{mod}\ 5) \\ & 17\equiv3\ (\mathrm{mod}\ 7) \end{aligned}\right.\]
计算 \(2^2\ \mathrm{mod}\ 5=4\),\(3^2\ \mathrm{mod}\ 7=2\),再由孙子定理由 \((4, 2)\) 推算得 9。
离散对数
由欧拉定理,有 \(a^{\phi(n)}\equiv 1\ (\mathrm{mod}\ n)\),若退化为一般形式 \(a^m\equiv 1\ (\mathrm{mod}\ n)\),如果 \(a\) 和 \(n\) 互素,则至少有一个整数 \(m\) 就是 \(\phi(n)\) 满足此式。称 \(m\) 为 \(a\ (\mathrm{mod}\ n)\) 的阶,或 \(a\) 所属的模 \(n\) 的指数,或 \(a\) 产生的周期长。
考虑固定 \(n\) 即模数,\(a\) 取不同值,观察 \(m\):
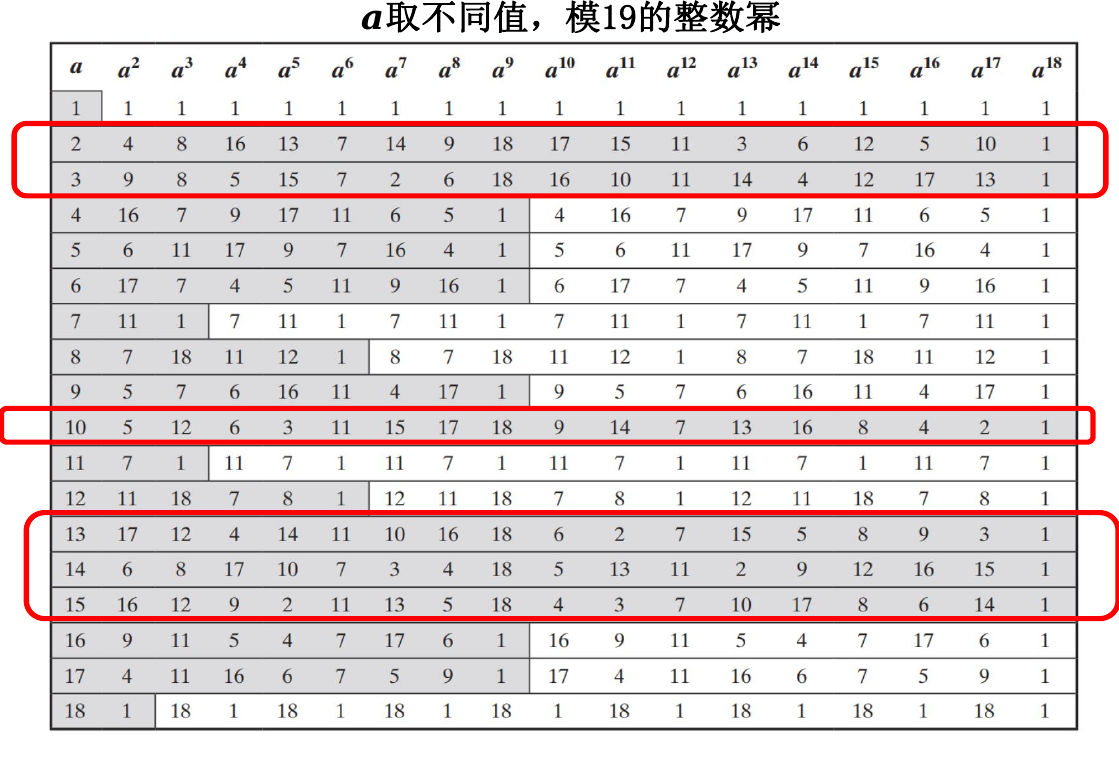
当 \(a\) 取 2,3,10,13,14,15 时,\(a\) 对模 19 的整数幂能产生模 19 的非零整数集,称这些数为模 19 的本原根。
对素数 \(p\) 的本原根 \(a\),\(a\) 的 1 到 \((p-1)\) 的各次幂产生 1 到 \((p-1)\) 的每个整数,即对任何整数 \(b\),有唯一的 \(i\) 使得
\[b\equiv a^i\ (\mathrm{mod}\ p), 1\leqslant i\leqslant (p-1)\]
这里的指数 \(i\) 称为以 \(a\) 为底模 \(p\) 的 \(b\) 的离散对数,记作 \(\mathrm{dlog}_{a, p}(b)\)。给定 \(a\)、\(i\) 和 \(p\),求 \(b\) 是容易的;但给定 \(b\)、\(a\) 和 \(p\),求 \(i\) 是非常困难的。
群、环和域
群
群 \(G\) 是定义了一个二元运算 \(\circ\) 的集合,满足下面的性质:
Closure 封闭性:\(\forall g, h\in G\),\(g\circ h\in G\)。
Associativity 结合律:\((a\circ b)\circ c=a\circ (b\circ c)\)。
Identity 单位元:\(\exist e\in G\),使得 \(\forall g\in G\),有 \(e\circ g=g\circ e=g\)。
iNverse 逆元:\(\forall g\in G\),总存在 \(g'\in G\),使 \(g'\circ g=g\circ g'=e\)。
如果 \(G\) 是有限的,称为有限群;否则称为无限群。在有限群中,\(G\) 的元素个数称为群的阶数,记作 \(|G|\)。如果群 \((G,\circ)\) 中的运算满足交换律,称为交换群或阿贝尔群。
如果 \(H\) 是 \(G\) 的子集,并且 \((H, \circ)\) 也构成一个群,称 \(H\) 是 \(G\) 的子群。
模 \(n\) 剩余类 \(Z_n=\{0, 1, \cdots, n-1\}\) 对模加运算构成一个群。取 \(Z_n\) 中与 \(n\) 互素的数作成集合 \(Z_n^*\),它对模乘构成一个群。
环
环 \(R\) 是定义了两个二元运算「加法」\(+\) 和「乘法」\(\times\) 的集合。关于加法,它是一个交换群,单位元为 \(0\),\(a\) 的逆元为 \(-a\);此外:
乘法封闭性:\(\forall a, b\in R, a\times b\in R\)。
乘法结合律:\(\forall a, b, c\in R, a\times(b\times c)=(a\times b)\times c\)。
分配律:\(a\times(b+c)=a\times b+a\times c\)。
若关于乘法满足交律,称为交换环。若存在乘法单位元 \(1\),并且不存在零因子即 \(\forall a, b\in R\),如果 \(a\times b=0\),则 \(a=0\) 或 \(b=0\),称为整环。
\((Z_n, +, \times)\) 构成一个环,但不一定是整环,如 \(Z_8\) 中 \(2\times 4\ \mathrm{mod}\ 8=0\) 存在零因子。
域
域 \(F\) 是一个这样的整环,它存在乘法逆元,即 \(\forall a\in F\),且 \(a\) 不为零元,则 \(\exist a^{-1}\in F\) 使得 \(a\times a^{-1}=1\)。即:
\(F\) 对加法构成交换群。
\(F\) 去除零元,对乘法构成一个交换群。
有限域
元素个数有限的域称为有限域。有限域的阶必须是一个素数的幂,即 \(p^n\)。阶为 \(p^n\) 的有限域一般记作 \(GF(p^n)\)。在密码学中,我们研究的「有限域」有两种:\(GF(p)\) 和 \(GF(2^n)\)。
对于有限域 \(GF(p)\),我们可以定义为 \(Z_p\) 即 \(\{0, 1, \cdots, p-1\}\),运算为模 \(p\) 的算术运算。由于 \(p\) 是素数,\(Z_p\) 中的每一个元素都与 \(p\) 互素,因此能构成一个有限域;但是对于 \(GF(2^n)\),无法直接用现成的数集来构造有限域。例如,当 \(n=3\) 即 \(GF(8)\) 时,\(Z_8\) 中并不是每个元素都与 8 互素(事实上 \(Z_8\) 不是整环)。
对于有限域 \(GF(2^n)\),我们使用系数在 \(Z_2\) 中的多项式模运算来构造有限域。