编译原理 4：句法制导翻译

在完成语法分析后，我们得到了源代码对应的语法树，但这样的东西距离能用来运行的机器码显然还有不少的距离。具体地，我们即使有了语法树，我们还是不知道代码的语义——代码「要做什么」。句法制导翻译关注的就是读懂代码的「语义」，使用 CFG 来引导对语言的翻译。

基本思想

我们为 CFG 中的文法符号设置语义属性，用来表示语法成分对应的语义信息。文法符号的语义属性值，是用与文法符号所在产生式相关联的语义规则来计算的。

需要引入句法制导定义（SDD）和句法制导翻译方案（SDT）。

句法制导定义

SDD 是对 CFG 的推广，它将每个文法符号和一个语义属性集合相关联，将每个产生式和一组语义规则相关联。

如果 \(X\) 是一个文法符号，\(a\) 是 \(X\) 的一个属性，则用 \(X.a\) 表示属性 \(a\) 在某个符号为 \(X\) 的分析树结点上的值。语义规则则是在产生式中，对某一语法变元的某个属性进行计算的规则。例如，对于 C 语言变量类型 \(T\to\mathrm{int}\)，它对应的语义规则就是 \(T.type=\mathrm{int}\)（将 \(T\) 的 \(type\) 字段设置成 \(\mathrm{int}\)）。

句法制导翻译方案

将语义规则（语义动作）嵌入 CFG，我们就得到句法制导翻译方案 SDT。我们把语义动作放在花括号内，如：

\[\begin{aligned} & D\to T\,\textcolor{blue}{\{L.inh=T.type\}}\,L \\ & T\to\mathrm{int}\,\textcolor{blue}{\{T.type=\mathrm{int}\}} \\ & T\to\mathrm{real}\,\textcolor{blue}{\{T.type=\mathrm{real}\}} \\ & L\to\textcolor{blue}{\{L_1.inh=L.inh\}}\, L_1, \mathbf{id} \end{aligned}\]

语法符号的属性

综合属性

综合属性是指只能通过一个语法符号（非终结符或者终结符）自身或者（非终结符）它的子结点属性值来定义的属性。例如，对于产生式 \(E\to E+T\)，对应语义规则 \(E.val = E.val + T.val\)，这里的 \(val\) 就是综合属性。

继承属性

继承发生是指只能通过非终结符的父结点、兄弟结点或者它本身属性值来定义的属性。例如，对于产生式 \(D\to TL\)，对应语义规则 \(L.inh=T.type\)（即 \(L\) 的类型是 \(T\) 给出的），\(inh\) 就是继承属性。

分析树和依赖图

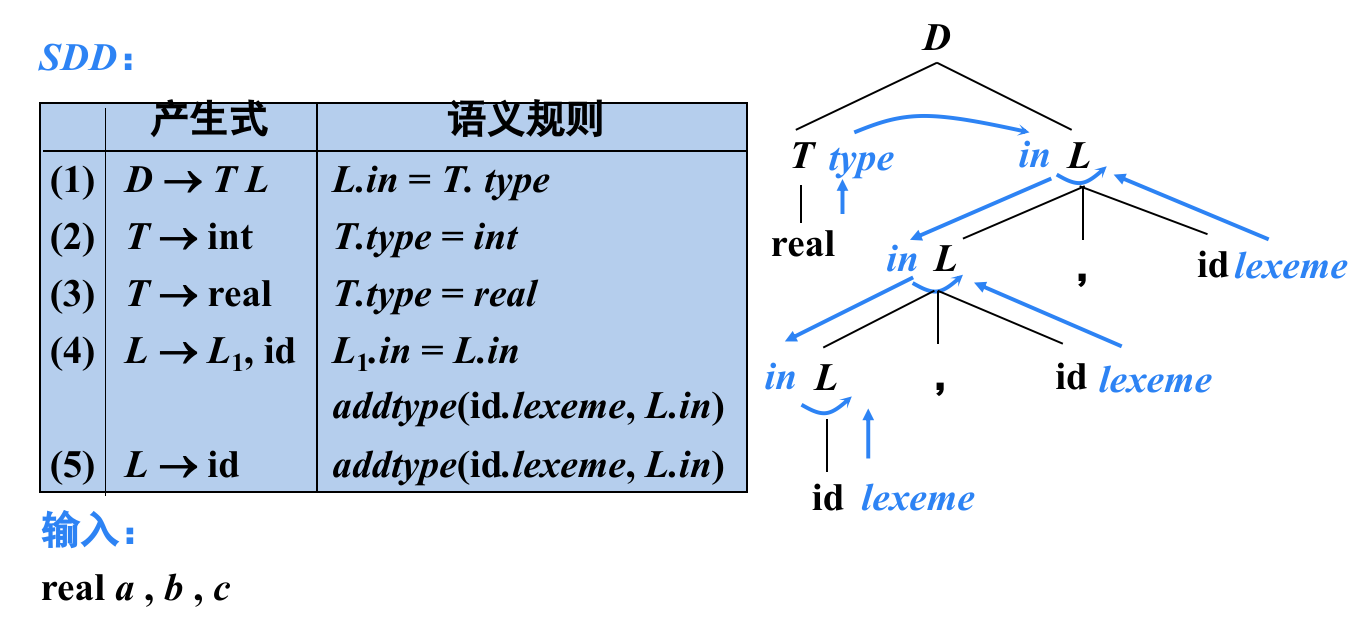
在语法分析树中，如果将结点（语法符号）的属性和属性之间的依赖关系画在树上，其中综合属性画在结点的左边，继承属性画在右边，我们就可以得到一个有向图，称为「依赖图」。如果属性 \(X.a\) 的值依赖于 \(Y.b\) 的值，则依赖图中有一条从 \(Y.b\) 到 \(X.a\) 的边。如：

S-SDD

仅仅使用综合属性的 SDD 称为 S-属性的 SDD，或 S-属性定义、S-SDD。由于综合属性只能通过节点自己或者子节点计算，对于这样的 SDD，可以按照分析树结点自底向上计算各个属性值。例如：

S-SDD 定义的制导方案（SDT），只要将对应的语义规则放置在对应的产生式末尾，例如：

如果这个文法可以使用 LR 分析，那么它的 SDT 可以在 LR 句法分析过程中实现：在规约发生时，执行相应的语义动作。在原有的状态栈和符号栈之上，我们增加一个「综合属性」栈，用来存放对应符号的综合属性值，即可实现 SDT 的 LR 分析。

具体地，我们还要将语义规则中的 \(\{A.a=f(X.x, Y.y, Z.z)\}\) 这样的抽象定义，更改为具体可执行的栈操作。例如：

stack[top - 2].symb = A
stack[top - 2].val = f(stack[top - 2].val, stack[top - 1].val, stack[top].val)
top = top - 2

当规约动作发生时，按这些栈操作进行即能实现 S-SDT 的语义分析。

L-SDD

使用了部分继承属性的 SDD 称为 L-SDD，其中 L 的意思是「从左到右」，即这种 SDD 依赖图的边可以从左到右，但不能从右到左。L-SDD 的属性要么是综合属性，要么是这样的继承属性：假设存在产生式 \(A\to X_1X_2\cdots X_n\)，其右部符号 \(X_i\) 的继承属性仅依赖于 (a) \(A\) 的继承属性，或 (b) \(X_1X_2\cdots X_{n-1}\) 的属性，或 (c) \(X_i\) 本身的属性，且不构成环路。

例如：

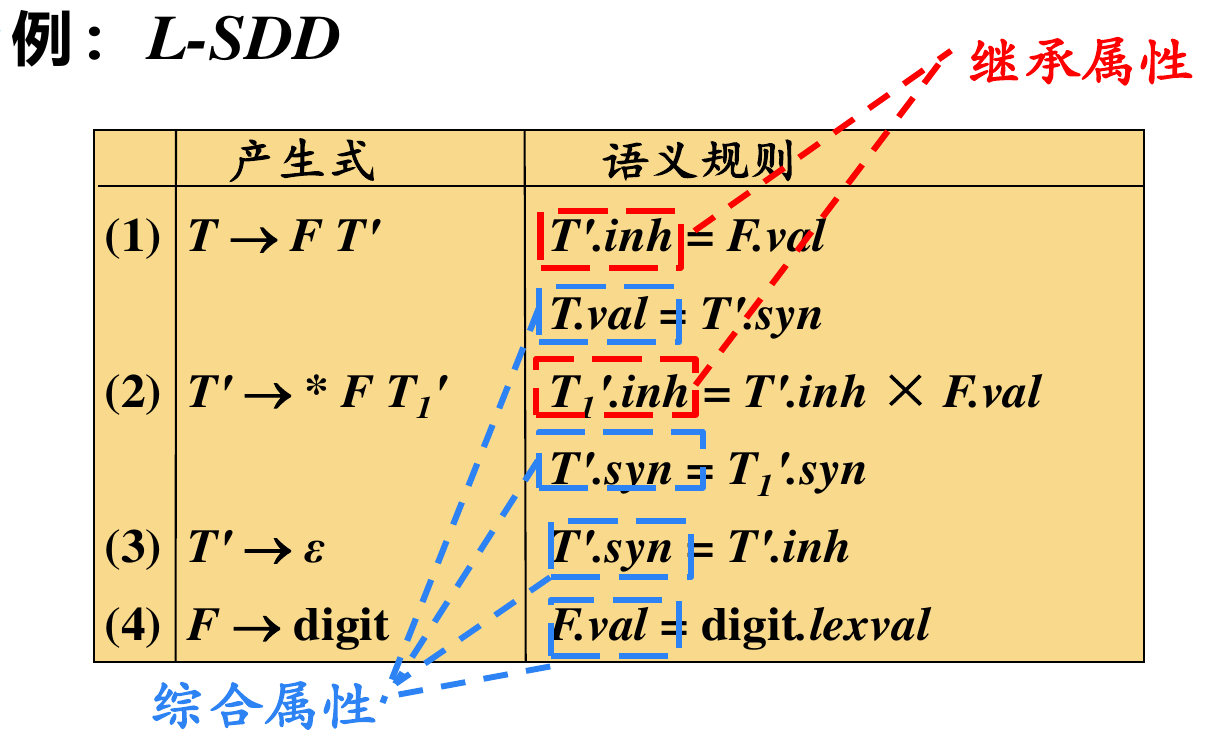
对于 L-SDD 的 SDT，需要：

将计算某个非终结符号 \(A\) 的继承属性的动作插入到产生式右部紧靠 A 的本次出现之前的位置。
将计算左部综合属性的动作放在最后。

例如：

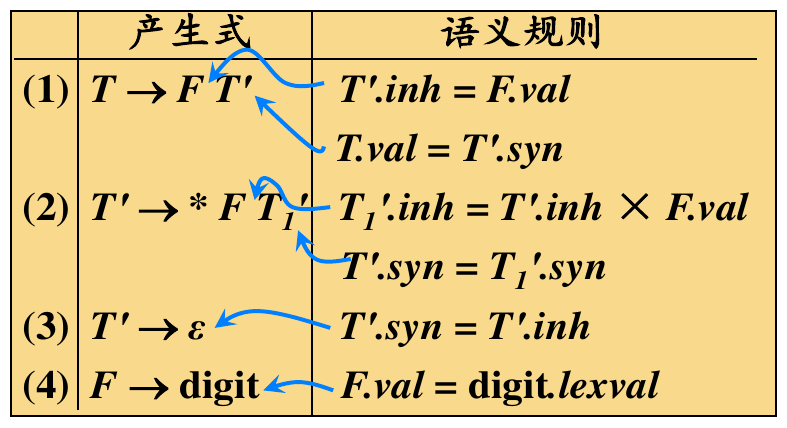
得到：

在非递归的预测分析中进行翻译

「非递归的预测分析」即 LL(1) 的分析法。在编译原理 2：自顶向下的语法分析中，我们使用「语法分析栈」记录已经分析出来的语法变元。现在，我们需要对这个栈中的元素进行扩充，将原先的单个文法符号 \(A\) 变成下面的结构：

以上面的乘法文法为例。首先，将所有的语义动作用指针指代，得到下面的 SDT：

尝试分析式子 3 * 5。首先，按照 LL(1) 分析表的构造文法，先写出这个文法的 LL(1) 分析表。

栈顶⬇️ 读入➡️	\(*\)	\(\mathbf{digit}\)	\(\#\)
\(T\)		\(T\to FT'\)
\(T'\)	\(T'\to*FT_1'\)		\(T'\to\varepsilon\)
\(F\)		\(F\to\mathbf{digit}\)

然后开始分析。

启动时，分析栈为初始符号 \(T\) 的综合属性和继承属性。
```
T   Tsyn   #
    (val)
```

读入 3，使用 \(T\to FT'\)，将 \(T'\) 和 \(F\) 先后入栈。

F   Fsyn  {a1}   T'    T'syn  {a2}  Tsyn  #
    (val)        (inh) (syn)  ===>  (val)

使用 \(F\to\mathbf{digit}\)，将 \(\mathbf{digit}\) 入栈，消去 3。

digit  {a6}  Fsyn     {a1}   T'      T'syn  {a2}  Tsyn  #
(3)    ===>  (val=3)  ====>  (inh=3) (syn)  ===>  (val)

读入 *，使用 \(T'\to *FT_1'\)，将 \(T_1'\)、\(F\) 和 \(*\) 先后入栈，消去 *。

*  F  Fsyn  {a3}   T1'  T1'syn  {a4}  T'syn  {a2}  Tsyn  #
      (val)       (inh) (syn)   ===>  (syn)  ===>  (val)
           (T'inh=3)

读入 5，使用 \(F\to\mathbf{digit}\)，消去 5。

digit  {a6}  Fsyn  {a3}  T1'  T1'syn  {a4}  T'syn  {a2}  Tsyn  #
(5)   ====> (val=5) 3*5=> (inh=15) => ...

L-SDD 的 LR 翻译

给定一个 LL 文法为基础的 L-SDD，可以修改这个文法来对它进行 LR 分析中的句法制导翻译。我们将每个产生式右部中间的语义动作移出，改为用产生 \(\varepsilon\) 的标记非终结符替代。这样在修改后的 SDT 中，所有语义动作都在产生式的末尾。如：

\[\begin{aligned} T&\to FMT'\ \{T.val=T.syn\} \\ M&\to\varepsilon\ \{M.inh=F.val, M.syn=M.inh\} \\ T'&\to *FNT_1'\ \{T'.syn=T_1'.syn\} \\ N&\to\varepsilon\ \{N.i1=T'.inh, N.i2=F.val, N.syn=N.i1\times N.i2\} \\ T'&\to \varepsilon\ \{T'.syn=T'.inh\}\\ F&\to \mathbf{digit}\ \{F.val=\mathbf{digit}.lexval\} \end{aligned}\]

然后，重新设计 LR 分析表，在规约动作发生时，执行相应的语义动作。

本节笔记到此结束。

计算机技术学习札记